

This is a hypothetical transcript of my keynote presentation at ACM REP ’24 in Rennes, France. It’s not an actual transcript of what I said. I wrote it mostly before the talk, so consider it something like a preprint. In addition, it contains references for further study that I did not necessarily mention orally.
My impression is that almost everyone at this conference has a background in computer science. That’s not my case. I am physicist, with a PhD in statistical physics, and for most of my career I have worked in molecular biophysics, in particular the structure and dynamics of proteins, using computational tools. I will thus describe R&R issues from the point of view of a computational scientist.
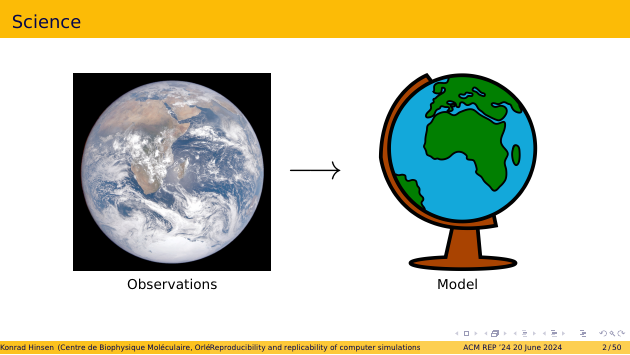
To set the context, let me start with a bird’s-eye view of science: it is a process that takes observations as inputs and produces a model of the world as its output. That model is of course very complicated, and also quite messy. It consists of a huge number of submodels for specific phenomena, but all these submodels are somehow connected.
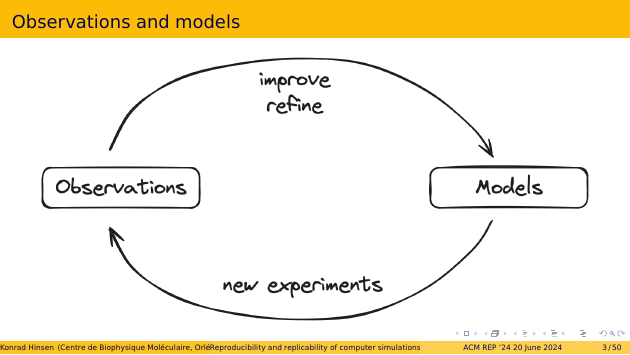
In this process, new observations are used to improve and refine existing models, and occasionally introduce new ones. What is perhaps less obvious is that the models are also crucial for making the next generation of observations. Few observations are made randomly nowadays. Most of them are the outcome of experiments that were carefully designed, based on our current models.

Models can take many different forms, but the ones we are interested in today are computational models. A computational model is a (usually partial) parameterized specification for algorithms that compute predictions, meaning theoretical values for quantities that can be observed in an experiment. At least in principle, because computational models are often used to compute values that are difficult or impossible to measure for technical or economic reasons.
The specifications in a computational model are derived from theoretical considerations, whereas the parameters, usually numbers, are derived from observations.
The relative importance of specifications and parameters can vary widely. In physics and engineering, there are strong and well-tested theories that lead to very constraining specifications, with only a small number of parameters. At the other end of the scale, Deep Learning uses weak theories to decide on an architecture of a neural network, which then has a huge number of parameters to learn from equally huge amounts of data.
For an in-depth discussion of computational models, see this article I wrote recently (or its free preprint).

There are three typical scenarios in computational science, although hybrids and combinations exist as well.
A simulation makes predictions from a model. A data analysis uses trusted models, meaning models that have stood the test of time, to interpret observational data. Data science uses generic models, i.e. weak-theory models with many parameters, in order to capture the salient features of complex datasets.

A side note: contrary to popular belief, data science is not a new idea. An early example is the use of epicycles to describe the orbits of the Sun and the planets as sean from Earth. Any periodic orbit can be described as a superposition of epicycles, so it’s just a matter of finding the parameters. This example shows that data science is the most primitive form of science, rather than an advanced stage as modern practitioners like to believe. The role of data science is to open up new topics of scientific inquiry with purely descriptive models that require little theoretical foundation.

My focus for today is on simulations. This lets me concentrate on reproducibility and replicability issues related to computational models, without being distracted by the issues associated with observational data. Nevertheless, everything I will say also applies to data analysis and data science, because they use computational models as well.

These are definitions for “reproducibility” and “replicability” that you have seen before: I copied them from the “call for papers” on the conference Web site. I will actually use modified versions of these definitions, so I’d better start by explaining them.
In the definition of “reproducibility”, I propose to replace “consistent results” by “bit for bit identical results”. I know that this is controversial, and the first part of my talk is actually dedicated to explaining why I consider this to be a more useful definition.
As for “replicability”, I merely add something that I think was simply overlooked. The definition from the call for papers provides different observational data as the only possible variability in explorations of replicability. This would mean that replicability cannot be an issue for computer simulations! I therefore add “different code”, or more generally methodological differences, as a second source of variability.
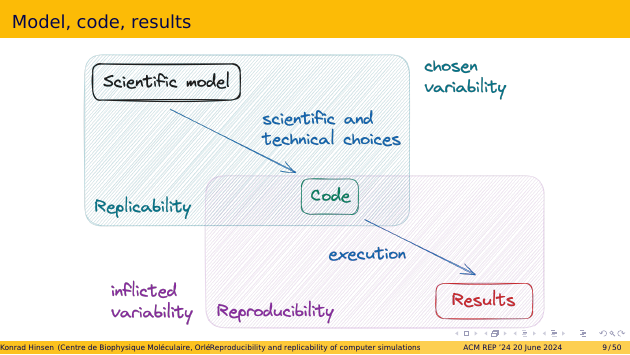
Let’s look at how these definitions apply to simulations. We start from a scientific model for the phenomena we want to simulate. Then we write code, a simulator, and in doing so we make various scientific and technical choices. For example, we choose specific algorithm where the scientific model only prescribes the result of a computation. And at the technical level, we need to choose a programming language in order to write any code.
Once we have the code, we execute it to obtain results. This involves various technical steps, for example compiling the code, or choosing the most appopriate computer architecture for the job.
Replicability is about the variability of the scientific and technical choices made in preparing the code. Reproducibility is about the variability of the infrastructure required for execution.
We tend to perceive reproducibility and replicability as distinct issues, which is largely due to the different nature of the variability involved. Replicability explores chosen variability, i.e. the different choices one can make in a scientific study. This has always been an important aspect of doing science. In contrast, reproducibility is about variability that is inflicted by the techical context, which scientists neither care nor know about very much. In most scientists’ minds, once a piece of code is completed, its results are fully determined and thus reproducible. That’s our mental models of computers as deterministic machines. It always comes as a bad surprise that this isn’t correct, and we often try to hide from the problem, preferring to sweep it under the rug rather than confront it and deal with it.

The situation in which reproducibility and replicability matter most in practice is the confrontation of incompatible findings.
Consider two players, individuals or teams, who work in the same field. They can be collaborators, competitors, or author/reviewer pairs.
Each player does some work and finds something relevant, but the two findings are in conflict: they cannot both be right. The findings can be observations, inferences, computed results, or conclusions drawn.
Assuming that both players can be considered competent and honest, and that the topic of the disagreement is of sufficiently wide interest, the question now is how to resolve the disagreement. Someone has to figure out why the two findings are incompatible. What are the relevant differences in the paths that led to them?
Those differences can come from both chosen and inflicted variability. Reproducibility and replicability both come into play. But what matters most of all is explorability. Each player must be able to dive into the work of the other, searching for scientific or technical differences.
It follows that purely technical reproducibility, as in “Here is my Docker container, you can rerun my code and get the same numbers.”, is not sufficient. The other player must be able to examine human-readable source code, not just a black-box container image. It’s often useful to have a container image, for convenience in first explorations, but it’s not enough.

I will now take a closer look at what computation actually is. Those of you with a computer science background may yawn and mumble something like “oh, Turing machines”. But please stay with me: I will discuss computation in the specific context of scientific research.
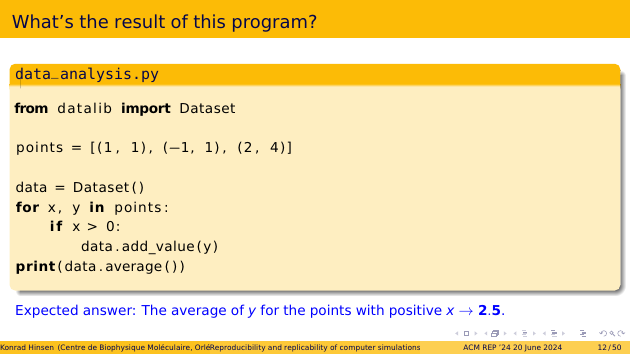
Let’s start with a small exercise for you. Here’s a short Python script. What is the result that it prints in the last line?
The script starts by defining three points in 2D space. It then adds the y values for the points with a positive x coordinate to a dataset. And then it computes the average of the datase.
The first and last points have positive x coordinates. Their y coordinates are 1 and 4. Their average is 2.5. That’s the result, right?
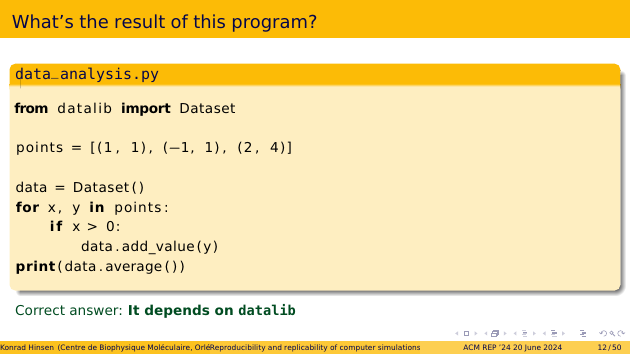
This is indeed the result that a human reader would expect. But the actual result can be different. In fact, we cannot know it from looking at the script. It depends on the code in the imported “datalib”. “Dataset”, “add_value”, and “average” are suggestive words for humans, but for Python they are just identifiers, without any particular meaning. Maybe “datalib” was written by a biology student just learning statistics, confused about the difference between averages and means, who ended up implementing the mean but calling it “average”!
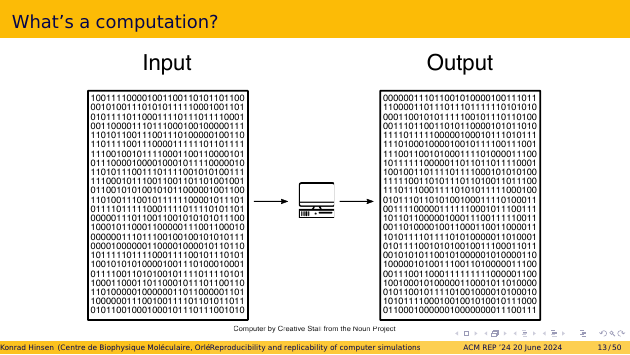
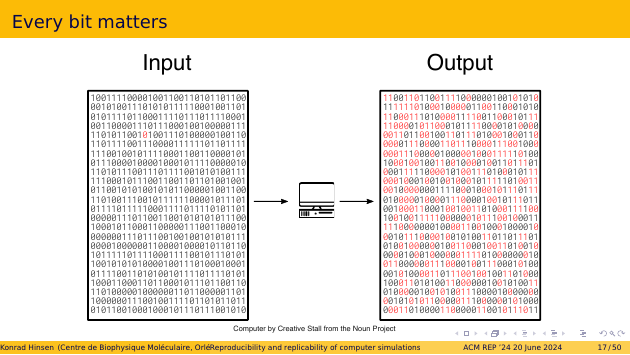
If we look at a computation at the lowest level, the inner workings of a computer, then it looks like this. You put some bit pattern into the computer’s memory, then you press a button to start the computation, and when it ends you find a different bit pattern in the memory. The transformation from input bit pattern to output bit pattern follows fixed rules and is deterministic.
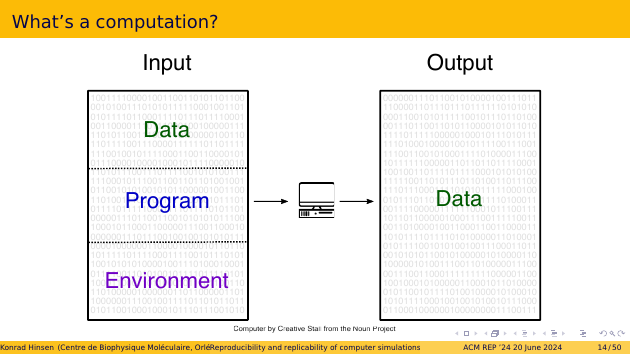
We humans like to divide the input bit pattern into data and code, and then further divide the code into a program and its environment. But this distinction is purely for human convenience. For the computer, it’s just bits. The distinction between the program and its environment is particularly weakly founded. The program is the code we care about, the environment is the code we don’t care about. But the computer doesn’t care what we care about.
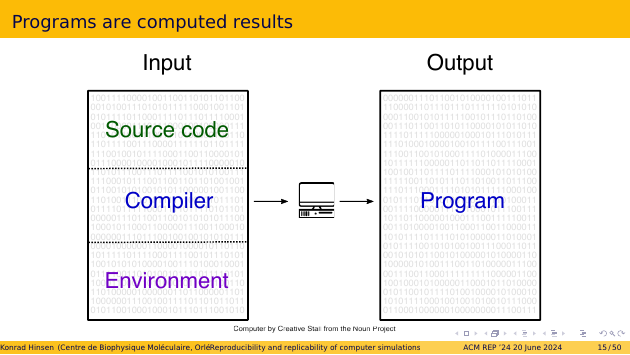
The program encoded as a bit pattern in the computer’s memory is usually not produced by a human programmer. We humans don’t like working with bit patterns. We write formalized text, called source code, and let a compiler transform it into an executable program. That process is just another computation. The compiler is part of the environment of our program, but it also needs its own environment for operating.
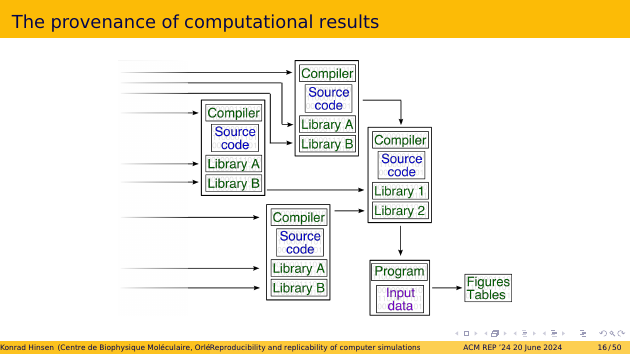
If we trace the provenance of all the bit patterns that we put into the computer’s memory, we get something like this. At the bottom right, we have the results we care about: the figures and tables for our next paper! It has been produced by a program and its input data. The program has been compiled, and combined with libraries. The compiler and the libraries have also been compiled from their source code. And so on. There is a lot more on the left side of this graph. And it’s not trivial at all to find a clear beginning to all of these computations - this is called the bootstrapping problem.
We see that what we consider to be “our” computation is just the final step in a long chain of computations. It’s the part we care about. But the computer cares equally about all the parts.
Computers are deterministic, by design. If you put the same bit pattern into the memory before pressing the button, then you get the same bit pattern at the end of the computation. If that doesn’t happen, we consider the computer defective. Reproducibility is thus guaranteed by construction at the bit level.
If we find different output and the computer is not defective, then there was also a difference in the input. We computed something else. A single bit flip in the input can suffice. There is no bound to the difference it can cause in the output, meaning that computation is chaotic.
Chaotic behavior is not desirable in engineered systems, though it is common in nature. Scientific instruments, in particular, are carefully designed not to be chaotic. The chaotic behavior of computers is tolerable only because they are so reliable. At the bit level, reproducibility really is a core feature of how we use computers.
For a more detailed discussion of chaotic behavior of computation, see this paper (or its free preprint).

Here are two 32-bit patterns. They differ in five positions, which I have highlighted in green. Are they similar? If they were results of two computations, would you say they are “consistent”?

The second line shows them in hexadecimal, grouping four bits into one letter. Does that make a difference to your judgement?
Next, decimal integers. The numbers you use in everyday life. Is the difference important?
Now let’s try single-precision floating-point. They are equal to three to four significant digits. Is that good enough?

Finally, let’s interpret them as Unix time stamps. On the left, you see the scheduled start of my keynote talk, on the right its end. The hour between the two time stamps is the most important hour in the history of civilization! These time stamps are not similar at all!
Similarity, approximate equality, or equivalence are all concepts that apply to the interpretation of a bit string in a given context, not to the bit string itself.

The bit manipulations in a computer are a specific kind of formal system. A formal system consists of rules about sequences of symbols. In a computer memory, the symbols are bits. More human-friendly formal systems use Unicode characters instead. A formal system has rules about syntax, which define which symbol sequences are valid expressions. It also has rules for manipulating sequences of symbols, such as performing integer arithmetic on bits.
The most important aspect of a formal system is that it’s a closed universe of symbols. There is no interpretation of the symbols as referring to something in the outside world. The rules for integer arithmetic are of course designed to correspond roughly to integer arithmetic from mathematics, but this correspondence is not perfect, and it’s not something the computer needs to know when manipulating bits.
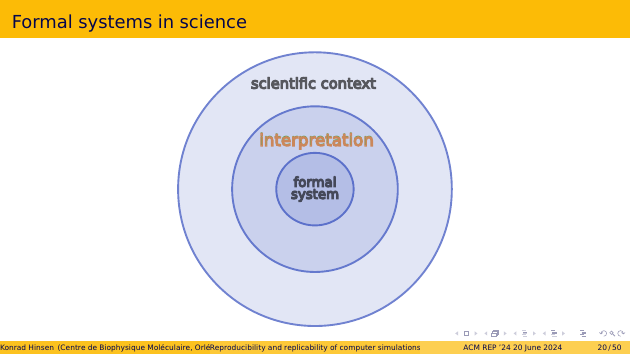
When we use formal systems, such as programs, in scientific research, we do it for some reason other than watching bits flip in the computer’s memory. We interpret the inputs, outputs, and transformations in terms of a scientific context. We decide to encode DNA sequences or temperature measurements as specific bit patterns, and design the rules of our program, i.e. our formal system, such that they represent scientifically relevant operations.
Humans are notoriously bad at distinguishing formal systems from their interpretations. We mix them up all the time. In human languages, all words have meanings that refer to context. When we see “average”, we think of a specific mathematical concept, rather than of an arbitrary seven-letter identifier. Programming languages are dangerous hybrids: for the computer, they define formal systems, whereas for humans, they express formalized statements about something, usually about the real world.

There is a nice case study by Sussman and Wisdom from the AI lab at MIT. The lab name is from the first wave of AI hype, not the current one, so they talk about symbolic computation. They analyse the common notation used for Langrangian mechanics, one of the many formulations of classical mechanics. It’s in every textbook for physics students. And yet, they show that the notation is ambiguous, that it makes no sense when you try to separate the notation from its interpretation. That is very common for mathematical notation in science. Then they introduce a new notation which is a formal language that you can manipulate by computer programs. This formal notation is much more powerful.

A similar observation had been made much earlier by Donald Knuth: the mere act of formalizing a scientific idea, with the computer forcing us to remain honest about our formalization, is helpful in understanding a complex topic.
So formal systems are very powerful tools in science, when used correctly. Just be careful not to mix them up with your interpretation.

Now let’s get back to defining reproducibility. If we define it at the bit level, we stay inside the formal system. A result then is identical to an earlier one, or it isn’t. This only requires comparing bit sequences, so it can be tested automatically by a computer. And we can ensure it with an appropriate computational infrastructure.
If all we ask for is “consistent” results, meaning that they are close enough for the scientific problem at hand, then we are at the level of interpretation. The answer depends on context, and requires expert judgement. This also means that we can do no better than verify a posteriori if two results are sufficiently similar. There’s no way to bake reproducibility into our infrastructure.
That’s why I propose that we go for the bit level. We can solve the reproducibility problem, and move on to more interesting things in science. For example replicability.
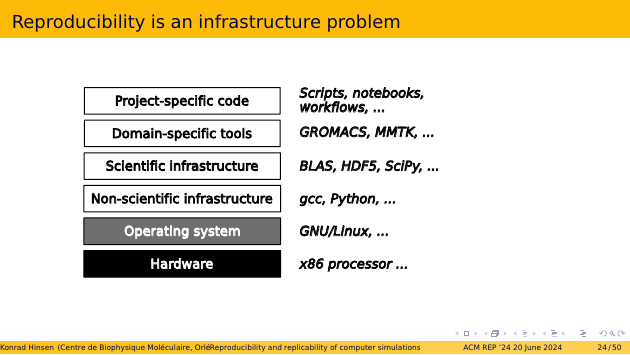
This figure shows a typical scientific software stack. On the bottom, we have the hardware, on top of which there’s an operating system that permits us to install and run our own software. Next, there’s a layer of infrastructure software that scientists share with other application domains. That’s where programming languages live, for example. On top of that, we have more specifically scientific infrastructure, which consists of mature and widely used software packages, e.g. for data management or basic number crunching. Up to here, we have software that scientists are vaguely aware of but don’t interact with very much. What we deal with every day is domain-specific tools from our discipline, and the scripts, notebooks, or workflows that we write as part of our research.
Since every layer depends on the layer below it, the only way we can get the outputs of the top layer to be reproducible, bit for bit, is by making the whole software stack reproducible, bit for bit as well. It is important to understand that there is no other way to guarantee reproducibility at the formal system level. If anything in the stack changes, your input bit patterns are different and the outputs are different as well, in general. There may well be changes in the software that make no difference for the final output, but unless you can prove that in each specific case, it’s just wishful thinking. There is no notion of similarity for software at the bit level. Version numbers in particular are outside of the formal system. They are not even an interpretation, they are merely the authors’ declaration of their intention.
For hardware, reproducibility is not much of an issue in practice, as long as we use commodity parts. Only for highly optimized software that exploits details of the hardware architecture, hardware can be a source of inflicted variability. But it’s already at the operating system level that reproducibility is usually lost. The architecture of our operating systems goes back to the 1970s, and it is based on the idea of a single computational environment per machine, which is extended and updated through manual intervention. So we need to replace this layer by something else.
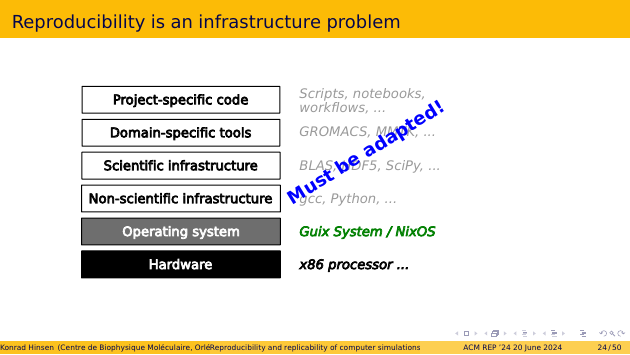
Fortunately, reproducible alternatives already exist. We even have two of them: Nix and Guix. They have both been mentioned yesterday in various talks. Both are based on the same principles, but implement them differently. In the following I will refer to Guix because that’s what I know and use, but you can mentally substitute Nix if you prefer.
The bad news about the new operating system layer is that all layers above it have to be adapted. All software is packaged as plug-ins to the operating system. If you hear that packaging software for Guix is hard, that’s not because Guix is complicated. It’s because Guix is different. The main work in packaging for Guix is figuring out where the software makes assumptions about the lower layers it depends on, and then patching the software to make those assumptions explicit, and adapt them to Guix.
If we want reproducibility to become the default, then we must write our software for reproducible operating systems from the start. It doesn’t matter much for which one, by the way. If you write for Guix, with all assumptions about dependencies explicit, then it’s much easier to translate to Nix, or some possible future reproducible OS. We can even envisage writing a compiler from Nix to Guix, or the other way round.
The difference between Guix and Nix on one side, and all other operating systems on the other side, is the same as the difference between Sussman and Wisdom’s classical mechanics compared to the traditional formulation. It’s a formal description vs. an informal one. It’s not a small detail, it’s fundamental progress in controlling software environments.

Making this transition is not a technical problem. It’s a socio-economic one. We have to make a transition from an inappropriate infrastructure to an appropriate one. This requires collective agreements followed by long-term investments. And that, in turn, requires institutions whose mission is to maintain a reproducible computational infrastructure for research.

Until we decide collectively to take responsibility for our infrastructure, we will remain stuck with workarounds. I will mention only the two most popular ones here.
The first workaround is to freeze computational environments as executable binaries, which we then distribute and archive. Today, the most popular medium for this is Docker containers, but you can do the same with virtual machine images, statically linked Linux binaries, maOS application bundles, etc. Virtual machine images are only choice that has a good chance of being long-term reproducible. But all of these techniques share the same problem: unless the binaries themselves are reproducible from source code, which they rarely are, you are providing reproducibility at the price of making replicability a lot more difficult to achieve. You cannot explore the impact of scientific choices if the only available artifact lets you neither see nor modify them.
The second workaround is cross-platform environment managers, the most popular of which is conda. They try to solve the reproducibility problem one level above the operating system. Since operating systems tend to change more slowly than the layers above them, this actually works for a while. For example, conda environments tend to remain reproducible for about six months. It is important to understand that, as long as there is someone who can pull the rug from under your feet, you cannot achieve the stability you need. In my field of research, computational biophysics, research projects often stretch over five years. We need reproducibility for at least twice that time span in order to be able to explore replicability issues.
Such workarounds are necessary today, because a reproducible infrastructure is not yet conveniently available to most computational scientists. But workarounds also take away resources and community attention from real solutions. One of the biggest obstacle to achieving reproducible infrastructure is the widespread belief that existing workarounds are good enough, or the best we can hope for.

In my abstract, I promised to answer a couple of questions. Let’s do that now.
First: Should computer simulations be made reproducible? Why? The answer is yes. If I cannot reproduce your simulation, then I don’t know what you have simulated and I cannot explore differences from my own work.
Second: To the last bit, or on a “good enough” basis? As I have explained in detail, bit for bit, because it is both more economical and more useful.
Third: At what cost? The cost is zero once we have suitable infrastructure and adapted our code to it. In other words, there is only a one-time investment cost. If we don’t, or aim for “good enough”, the cost may well remain high forever.
Four: Can we ensure reproducibility without repeating lengthy computations? Yes, if we let infrastructure take care of it.

The replicability questions make for a nice transition to the second part of my talk.
First: Is replicability more or less important than reproducibility in scientific practice? That’s not a useful question, because we need both, and both are related. You cannot explore replicability issues unless you have reproducibility. Put differently, you cannot explore variability choices as long as some variability is inflicted and out of your control.
Second: How replicable are computer simulations today?
Third: What are the obstacles to better replicability?
That’s what I will discuss now.
Here’s the replicability part of my schema again. Reminder: replicability is about the variability that comes from scientific and technical choices made on the path from science to code.
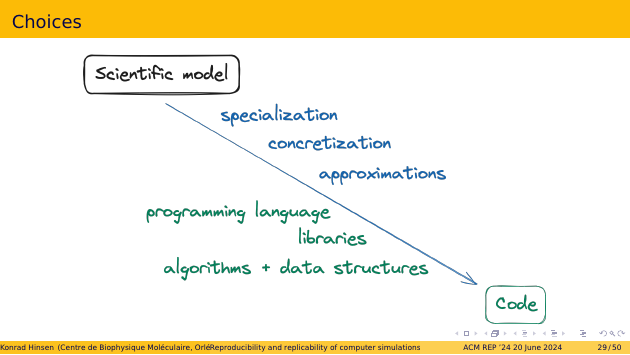
Let’s zoom in a bit and look at what those choices are. On the scientific side, the first kind of choice is specialization. Your scientific model can be quite general, but your code handles only a subset of what it could possibly apply to. For a user, this is important to understand, to avoid using the code for systems that are outside of its scope.
Next is concretization. Your scientific model may contain some aspect that is conceptually well-defined but not operationally. For example, the model may say that you have to compute an average over a probability density. There are many ways to do this, for example Monte-Carlo sampling. It may turn out that Monte-Carlo sampling is a good choice for some systems but a bad one for others. Therefore it matters that users of the code are aware of such concretization choices, and can change them.
The third kind is approximations. These are modifications to your model that make it worse, in exchange for some gain elsewhere. One such gain is being able to actually compute a result. Another frequent one is speeding up a computation. Approximations almost always imply specialization, because the approximation is better for some systems than for others. Again that’s something that users of the code need to know.
Now let’s move to the technical side. To write any code, you have to choose a programming language. Next, for anything but the simplest programs you choose libraries that perform some of the work. And then you have to design and implement algorithms and data structures that are a good fit to your job. In an ideal world, all these choices should be orthogonal to the science in your model and code. They would perhaps influence performance, but not results. In the real world, they do.
The main reason for this is that scientific and technical choices are not made independently, although that’s something scientists don’t like to admit. In reality, we don’t make scientific choices first, and then write the code. Rather, we start writing the code, discover that there’s a great library for a part of the job, but it requires some approximation. And then we accept that approximation without making much noise about it. The outcome is a scientific choice visible only in the code. A good recipe for replicability issues.
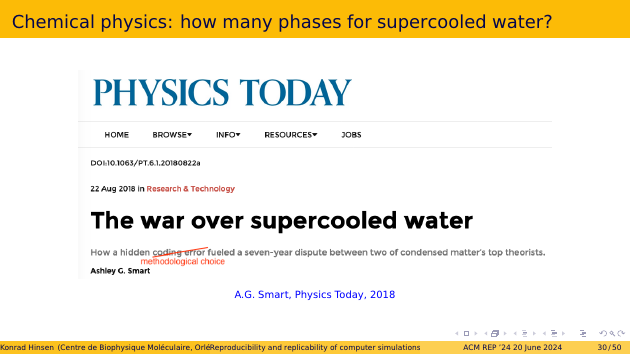
This story is a nice illustration. I encourage you to read it. It’s the story of a seven-year dispute between two research groups working on the same problem, but finding incompatible results. The story has all the spicy ingredients of real life, such as strong personalities and the bad disciplinary habit of not sharing code. It’s nicely told by a science journalist, who unfortunately misidentified the nature of the ultimate cause. It was not a “hidden coding error”, but an undocumented concretization choice.

I won’t go into the details here, but only highlight the two sentences from the article that clearly point towards an algorithmic choice, and not an error, as the cause for the disagreement.

This is a good moment to pause and think about what “replicable” actually means. Here is my proposal: A scientific finding is replicable if it is robust under irrelevant changes. Robust means equivalent given the current scientific state of the art. It’s a concept similar to “good enough”, or “consistent”. The more interesting part is “irrelevant”. Who decides what’s relevant? The scientific community of course. And the consensus, or its absence, on this question evolves over time, as the community learns.
And that is the reason why replication studies are important. They test the relevance of specific choices. They also expose tacit choices, i.e. choices that were not properly documented because they seemed obvious. More generally, they explore the space of variability.
The key aspect of replicability is therefore a precise documentation of all choices that were made, in a way that allows others to explore variations.
Replicability in my own domain, biomolecular simulation, is in a similar state as for simulations of supercooled water. I know my own field much better, so I use it for explaining where the difficulties come from. I’ll start with a brief overview of how these simulations work.
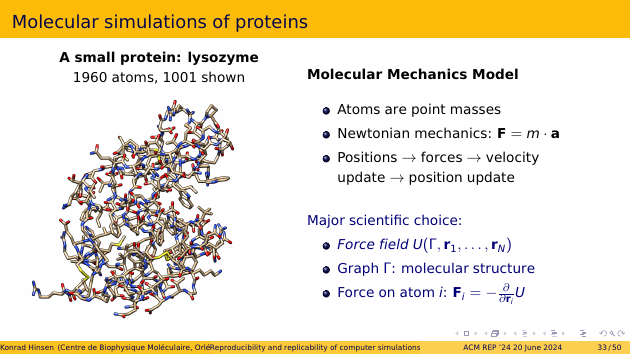
Consider a simple example, lysozyme. It’s a popular test case protein, both in the wet lab and in the computer. Lysozyme is part of many animal’s immune system. It destroys the cell wall of a certain kind of bacteria. It’s present in egg white, which makes it cheap to isolate in large quantities. Humans also make lysozyme, for example in tears. For my purposes today, lysozyme is nice because it’s small: about 2000 atoms. Most proteins are much bigger than that. The picture shows only about half of them. It is customary not to show hydrogen atoms, for clarity. With only a single chemical bond, they don’t contribute much to structural patterns. They just “hang off” the other atoms.
The most widely used scientific model in protein simulations is called “molecular mechanics”. It describes atoms as point masses that obey the laws of Newtonian mechanics. That’s grossly incorrect, but works much better than one should expect. A protein simulation thus works much like a simulation of planets orbiting the sun: from the atom positions you compute forces, the forces are used to update the velocities, and the velocities are then used to update the positions. You do that many many times and watch what happens.
The major scientific choice in molecular mechanics is the “force field”, which describes how the forces are computed from the molecular graph and the atom positions.

This is how a biomolecular force field is typically described in the scientific literature. The one I am discussing is called Amber, but others are not fundamentally different. There are five different contributions, each of which describes one aspect of atomic interactions: bonds, bond angles, dihedral angles, Lennard-Jones interactions, which summarize quantum effects, and electrostatic interactions.

The problem with that description is that it’s incomplete and ineaxct. Many details are missing. For example: how exactly do you sum over “all bonds” etc.? There are also idealizations, where a real simulation requires additional approximations in order to be manageable. For example, summing over all pairs of atoms is very slow, and not much better than approximations that are linear in the number of atoms. There are entire papers on such approximations, but the one that has actually been used in a given simulation can be very difficult to identify.

And then there’s the question of the numerical parameters in these equations. There are lots of them, and they are available as machine-readable files in weakly documented file formats. But how do you figure out the correct value for each term in the big formula? The answer is: by applying a graph-walking algorithm on the molecular graph. That algorithm is not documented other than by the source code.

The title of this paper on the Amber simulation software illustrates the difficulty faced by an ambitious explorer: how do you even find that algorithm in a multimillion-line code? There is an added difficulty not clear from the title: the code is also proprietary. You can get the source code, but you have to pay for it and sign some legal documents.
All this explains why replicability of biomolecular simulations is still very weak. There has been a lot of progress over the last years. Recent simulation software is Open Source, and people increasingly publish some of the input parameters and scripts they used. But that material is not reviewed, and in practice never suffices to answer all relevant questions.
Here is a personal story about the consequences of this sad state of affairs. A couple of years ago, I was working with a team of experimentalists on the structure of peptides in gas phase. The question we wanted to explore is whether a certain family of peptides adopts a helicoidal or a globular structure.
This is a rather exotic field, meaning that there are not many published studies. The one that everyone referred to was a few years old and concluded that some peptide sequences end up helicoidal, and others globular. Unfortunately, my own simulations resulted in globular structures for all of these sequences!
We couldn’t move on without understanding this difference. We could never publish results that disagree with the most cited paper on the topic without proposing an explanation.

First we set out to read the paper very carefully, but that didn’t get us very far. Here are some quotes that illustrate the level of precision.
The MACSIMUS suite of programs is still around, but the oldest available version is more recent than that paper. So it doesn’t really matter that the paper doesn’t quote a version number: I know that I wouldn’t be able to find it. CHARMM is another force field, like Amber. Its version 21.3 has two different parameter sets, for different model variants. Which one was used? I don’t know.

The description of the simulation strategy is so vague that it’s practically useless. But I must emphasize that I am not trying to criticize this specific paper. This level of description is the norm in my field. My own papers were no better until recently.

The core issue of replicability is the huge variability space, which makes it difficult to document all choices, and sometimes even to be just aware of them.
There are too many details to document in a paper. An exhaustive list would be a pain to compile but also to read, and verifying it against the reality of the code is practically impossible.
The executable code is a formal system, which guarantees completeness. All choices are in it, somewhere. But code is too low-level and technical as a documentation for humans. It is of course always possible to dig into the code and look for a specific problem, as the supercooled water story shows. But that’s an exceptional effort made in an exceptional situation. And the code was presumably much simpler than typical protein simulation software.

A useful perspective is considering replicability as a human-computer interface problem. The computer can easily keep track of many details, but humans can’t. And yet, it’s only humans who can appreciate the scientific impact of these details.
What if we could place the full variability space at the human-computer interface? Make it fully accessible to human consultation, but also to machine processing?
We already have a similar situation with knowledge graphs, which could be a source of inspiration. But there is an important difference as well: knowledge graphs are about established, published knowledge, whereas the variability space in computer simulations is subject to active exploration.
One key aspect is that the human and the machine interpretation of the variability space must be compatible. The human interpretation of the formal systems must match their operational semantics. That’s something that only human experts can verify, because computers cannot handle the interpretation. Now I can almost hear some of you mumbling “AI will solve this.” Maybe. As of today, it doesn’t, and I am rather skeptical. I am much more optimistic about AI supporting human experts in this task.

The hard part in getting there is abandoning our currently dominant view of simulation programs as machines for which scientists are operators. The user interface of a machine is too simple to cover our variability space.

We have to move towards a view of scientific models as data rather than code, and place this data at the user interface of interactive tools, much like in CAD, or in spreadsheets.

Moving “beyond programs” is an old idea, as shown by this 1979 paper by Terry Winograd. His vision remains compelling, but hasn’t been realized yet.
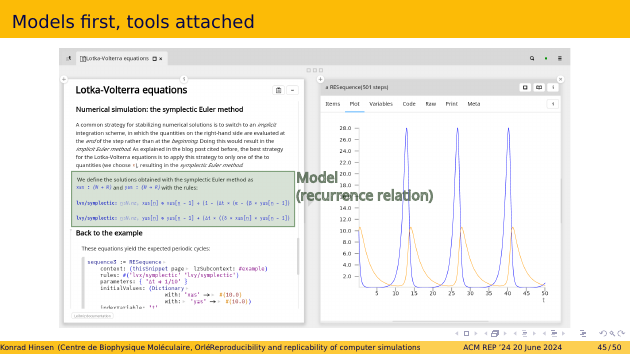
I have been working on this idea for a while, and here I show you screenshots of my current prototype. It’s not yet sufficiently advanced to handle really complex models such as biomolecular simulations. The example here is a very simple simulation of the Lotka-Volterra equations, which is one of the oldest models in ecology. It describies how the populations of two species, a prey species and its predator, evolve over time.
What looks like mathematical equations, typeset in blue, is actually the model, a discretized form of the Lotka-Volterra equations, written in a formal language that is fully machine-readable. You can click on each equation to explore it. It’s not just blue text.
You can look at this example here, but it’s a static rendering in which you cannot run the simulation. For that you need to download and install the code. But even from the static rendering, you can see the Wiki-like structure of the model, and explore all its dependencies. And this four-minute demo video shows what you can do in the interactive version.
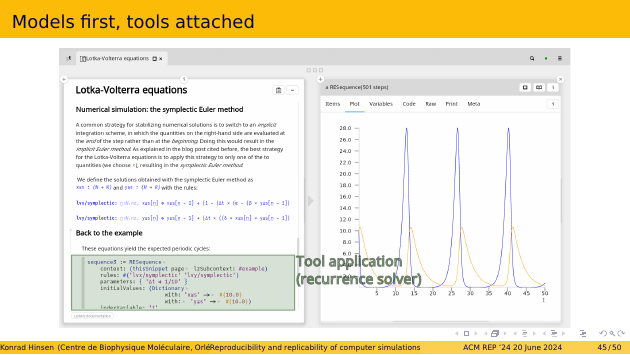
Below the equations, you see the code that runs the simulation, of which the results are shown on the right pane. The code calls a very generic tool, a solver for recurrence equations. There is almost no science in the tool, it’s all in the model. The tool scans the page and extracts the equations and their parameters from it.

I call my formal language a “digital scientific notation”, to emphasize its intended usage scenarios. It’s a formal language, and thus machine-readable and machine-searchable.
But it’s not a programming language. It is intended for encoding models and their specializations, concretizations, approximations, etc.
Models written in this language are data, not code. They can express algorithms, but not the operational aspects of a program, such as performing input or output.
For those of you who are into formal methods, a digital scientific notation is, technically speaking, a specification language. But I avoid this term because it suggests specifying a software system, which is not the intended use case.
For more details on digital scientific notations, see these two papers: - Scientific notations for the digital era - Verifiability in computer-aided research: the role of digital scientific notations at the human-computer interface

Digital scientific notations could be used in several ways. The easiest one to realize is their use in the documentation of scientific software. This would embed machine-readable models into prose written for humans. Human readers could check the conformance to established scientific knowledge, and computers applying formal methods could prove the equivalence to the code that’s actually run.
In a second step, digital scientific notations could become part of the software’s user interface, for example to perform specializations. Code generators could use the formal specification to produce optimized code.
The most futuristic scenario has scientists working with models in a computational medium, such as the Wiki-like evnironment of my prototype. Computational tools become plug-ins, accessible via user interface elements.
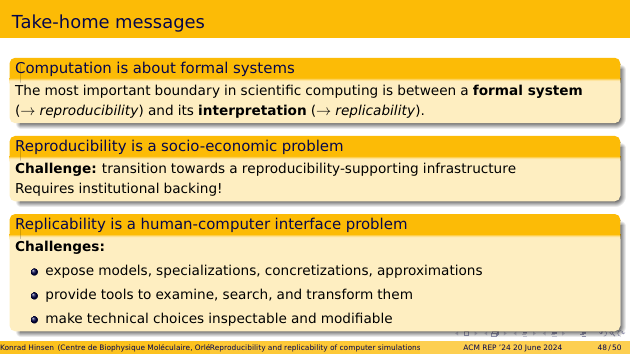
Congratulations, you made it to the end of my talk! Here are the three messages I would like you to remember:
It is important to understand the fundamental role of formal systems in scientific computing. The most important boundary is between a formal system and its interpretation. This boundary corresponds to the distinction between reproducibility and replicability.
Reproducibility is a socio-economic problem. The challenge is to transition towards an infrastructure that supports reproducibility. This requires institutional backing.
Replicability is a human-computer interface problem. The challenges involve exposing models and their specializations, concretizations, and approximations at the interface, which also provides tools to examine, search, and transform them. Technical choices must be inspectable and modifiable.
I’ll end with a page of advertising: There’s a new MOOC on reproducible research practices for scientific computation at scale, of which I happen to be one of the authors. It’s open until September 12. For more information, click here!